Altın oran nedir? Altın oran nasıl hesaplanır?
Güncelleme Tarihi:
Binlerce yıldır mükemmel güzelliğin gizli formülü olduğu düşünülen altın oran günümüzde de geçerliliğini koruyor. Bir mükemmeliyet ölçütü olan altın oran, Antik Yunan döneminden beri kullanılıyor. Peki, altın oran nedir? Altın oran nasıl hesaplanır?
Altın oran, matematik ve sanatta, bir bütünün parçaları arasında gözlemlenen, uyum açısından en yetkin boyutları verdiği sanılan geometrik ve sayısal bir oran bağıntısıdır. Eski Mısırlılar ve Yunanlar tarafından keşfedilmiş, mimaride ve sanatta kullanılmıştır.
ALTIN ORAN NASIL HESAPLANIR?
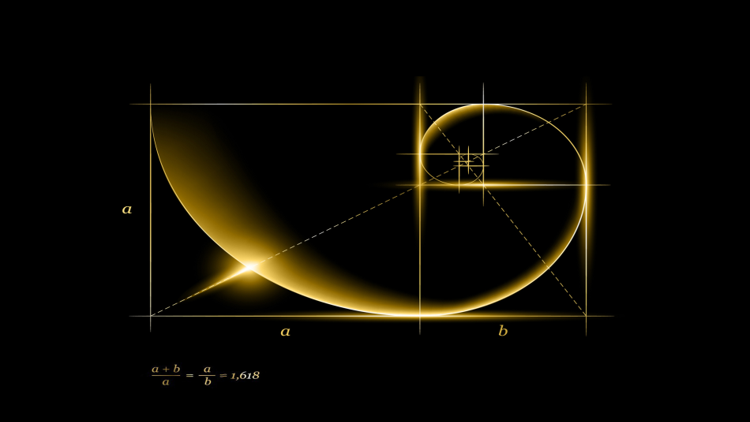
Bir doğru parçasının |AB| Altın Oran'a uygun biçimde iki parçaya bölünmesi gerektiğinde, bu doğru öyle bir noktadan (C) bölünmelidir ki; küçük parçanın |AC| büyük parçaya |CB| oranı, büyük parçanın |CB| bütün doğruya |AB| oranına eşit olsun.
Altın Oran, pi (π) gibi irrasyonel bir sayıdır ve ondalık sistemde yazılışı; 1,618033988749894...'tür. -noktadan sonraki ilk 15 basamak- Bu oranın kısaca gösterimi: {\displaystyle {\frac {1+{\sqrt {5}}}{2}}}{\displaystyle {\frac {1+{\sqrt {5}}}{2}}} olur. Altın Oranın ifade edilmesi için kullanılan sembol, Fi yani Φ'dir.


